
Kazalo:
- 1. korak: Ustvarite matriko NxN enotnih kvadratov
- 2. korak: Naključno nastavitev omrežja
- 3. korak: Pridobite nove razdalje
- 4. korak: Izberite točko in primerjajte razdaljo od te točke do drugih
- 5. korak: Premaknite se na novo točko
- Korak 6: Sila = K*razdalja
- 7. korak: Spremenite gibanje omrežja zaradi premaknjene točke
- 8. korak: Končana koda
- Avtor John Day day@howwhatproduce.com.
- Public 2024-01-30 12:07.
- Nazadnje spremenjeno 2025-01-23 15:09.

Celice lahko medsebojno delujejo z okoliškim zunajceličnim matrikom (ECM) in lahko delujejo tako, kot se odzivajo na sile, ki jih izvaja ECM. Za naš projekt simuliramo medsebojno povezano mrežo vlaken, ki bi delovala kot ECM, in vidimo, kako se omrežje spreminja kot odziv na premikanje ene od točk. ECM je modeliran kot medsebojno povezan sistem vzmeti, ki so sprva v ravnovesju z neto silo nič. Ker sila deluje na omrežje kot odziv na gibanje točke, poskušamo doseči, da se povezane točke odzovejo na silo tako, da se poskušajo vrniti v ravnovesje. Sila se spremlja z enačbo F = k*x, kjer je k konstanta vzmeti in x sprememba dolžine vlaken. Ta simulacija lahko pomaga pri splošnem razumevanju širjenja sil v vlaknatih omrežjih, ki jo lahko sčasoma uporabimo za simulacijo mehanotransdukcije.
1. korak: Ustvarite matriko NxN enotnih kvadratov


Za začetek kode izberemo N, ki bo določila dimenzije našega omrežja (NxN). Vrednost N lahko ročno spremenite, da po potrebi spremenite dimenzije omrežja. V tem primeru je N = 8, torej imamo mrežo točk 8x8. Ko generiramo matriko, povežemo vse točke v matrici, ki imajo dolžino 1 enote, s formulo razdalje, distance = sqrt ((x2-x1)^2+(y2-y1)^2). S tem dobimo mrežo kvadratov, ki so vsi enako razmaknjeni za 1 enoto. To je razvidno iz slike 101.
2. korak: Naključno nastavitev omrežja


V tem koraku želimo naključno razporediti vse lokacije točk, razen zunanjih točk, ki bodo tvorile našo mejo. Če želite to narediti, najprej poiščemo vse matrične koordinate, ki so enake 0 ali N. Te točke tvorijo mejo. Za mejne točke je lokacija naključno izbrana tako, da se na položaje x in y doda drugačna naključna vrednost od -5 do.5. Narisana naključna slika je prikazana na sliki 1.
3. korak: Pridobite nove razdalje

Ko vzpostavimo naše naključno omrežje, znova poiščemo razdaljo med povezanimi točkami po formuli razdalje.
4. korak: Izberite točko in primerjajte razdaljo od te točke do drugih



V tem koraku lahko s kazalcem izberemo zanimivo točko, kot je prikazano na sliki 2. Kazalec vam ni treba natančno premakniti na točko, ker ga bo koda prilagodila na najbližjo povezavo. Če želite to narediti, najprej izračunamo razdaljo med vsemi povezanimi točkami in točko, ki smo jo pravkar izbrali. Ko so izračunane vse razdalje, izberemo točko z najmanjšo razdaljo od izbrane točke, da postane dejansko izbrana točka.
5. korak: Premaknite se na novo točko



V tem koraku z uporabo točke, izbrane v prejšnjem koraku, premaknemo točko na novo mesto. To premikanje se izvede z izbiro novega položaja s kazalcem, ki bo nadomestil prejšnji položaj. To gibanje bo uporabljeno za simulacijo obremenitve zaradi spremembe dolžine vzmeti. Na vsej modri sliki je izbrana nova lokacija. Na naslednji sliki je gibanje mogoče prikazati z oranžnimi povezavami, ki so nove lokacije, v nasprotju z modrimi povezavami, ki so bile stare lokacije.
Korak 6: Sila = K*razdalja

V tem koraku uporabimo silo enačbe = k*razdalja, kjer je k konstanta 10 za kolagenska vlakna. Ker se optično omrežje začne v ravnovesnem stanju, je neto sila 0. Ustvarimo ničelni vektor dolžine matrike, ki smo jo ustvarili prej, da predstavlja to ravnovesje.
7. korak: Spremenite gibanje omrežja zaradi premaknjene točke




V tem koraku simuliramo gibanje omrežja kot odziv na premik točke, da se vrnemo v stanje ravnovesja. Začnemo z iskanjem novih razdalj med dvema točkama. S tem lahko ugotovimo spremembo dolžine vlaken, če pogledamo razliko med staro in novo razdaljo. S primerjavo novih in starih lokacij točk lahko vidimo tudi, katere točke so se premaknile, in tudi točke, s katerimi so povezane. To nam omogoča, da vidimo, katere točke bi se morale premakniti kot odziv na silo. Smer gibanja je mogoče razčleniti na njene komponente x in y, kar daje 2D smer vektorja. Z vrednostjo k, spremembo razdalje in vektorjem smeri lahko izračunamo vektor sile, ki ga lahko uporabimo za premikanje točk proti ravnotežju. Ta del kode izvedemo 100 -krat, vsakič se premikamo v korakih Force*.1. Izvajanje kode 100 -krat nam omogoča, da sčasoma spet dosežemo ravnovesje in z ohranjanjem mejnih pogojev vidimo spremembo v omrežju namesto preprosto celotnega premika. Gibanje omrežja je prikazano na sliki 3, pri čemer so rumene premikane pozicije, modra pa prejšnja.
8. korak: Končana koda
V tem razdelku je priložena kopija naše kode. Prilagodite ga svojim potrebam z modeliranjem različnih omrežij!
Priporočena:
USB JOYSTICK NIČEGA ZAMADA - SAMODEJNI ANALOGNI SPREMEMB: 5 korakov

USB JOYSTICK ZERO DELAY - SAMODEJNA ANALOGNA SPREMEMBA: To je dodaten projekt k spremembi resnične analogne krmilne palice Zero Delay USB Encoder. Pred dodajanjem te naprave morate kodirnik uspešno spremeniti, preizkusiti in umeriti. Ko končate in delate
Uporabite silo in si ustvarite svoj svetlobni meč (rezilo): 9 korakov (s slikami)

Uporabite silo in si naredite svoj svetlobni meč (rezilo): to navodilo je namenjeno izdelavi rezila za svetlobni meč Ben Solo Legacy Lightsaber, kupljenem pri Disneyland's Galaxy's Edge v Anaheimu v Kaliforniji, vendar lahko storite podobne korake za izdelavo lastnega rezila za drugačno svetlobni meč. Sledite za
Grafiranje temperaturnih sprememb zaradi podnebnih sprememb v Pythonu: 6 korakov
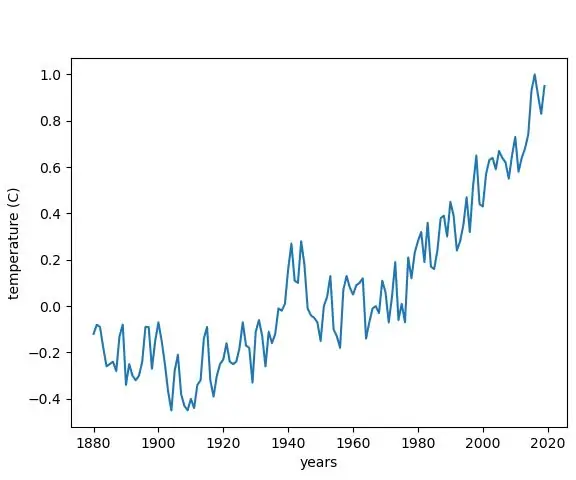
Grafiranje temperaturnih sprememb zaradi podnebnih sprememb v Pythonu: Podnebne spremembe so velik problem. In veliko ljudi zdaj ne ve, koliko se je povečalo. V tem navodilu bomo prikazali temperaturne spremembe podnebja zaradi podnebnih sprememb. Za goljufijo si lahko spodaj ogledate datoteko python
S silo razširite praznično veselje!: 5 korakov

Uporabite silo za širjenje prazničnega veselja!: Ta navodila vam bodo pokazala, kako sestaviti namizno božično drevo iz pisarniškega materiala, dodati mikro krmilnik in posamezno naslovljive LED diode ter nato uporabiti pas Sphero Force (izšel z drugo generacijo Sphero BB -8 droid) za tur
Kako napisati brutalno silo za številke (Visual BASIC 2008 Express): 5 korakov

Kako napisati grobo silo za številke (Visual BASIC 2008 Express): V tem navodilu vam bom pokazal, kako napisati tako imenovano "brutalno silo" v Visual BASIC 2008 Express, ki ga lahko prenesete tukaj -> http://www.microsoft.com/eXPress/download/ Sila je grozljiv " razpokanje " program, ki je zlomil
