Rekurzivno povzemanje matrike v Javi: 9 korakov

2024 Avtor: John Day | [email protected]. Nazadnje spremenjeno: 2024-01-30 12:03

Rekurzija je zelo uporaben in časovno učinkovit postopek, ki lahko hitro reši problem z zelo malo kode. Rekurzija vključuje način, ki ga ustvarite sami, in skrajša prvotno težavo.

V tem primeru bomo seštevali niz 10 celih števil, vendar je lahko velikost poljubne dolžine.

Zaloge

Poznati morate osnovno skladnjo java in imeti IDE ali urejevalnik besedil, ki bo napisal vašo kodo za to nalogo.

1. korak: Nastavite svojo glavno metodo

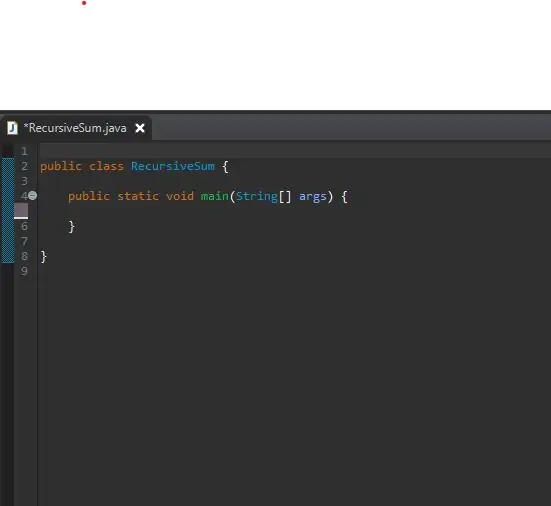
Za začetek nastavite svojo glavno metodo v novo ustvarjenem razredu. Svoj razred sem poimenoval Rekurzivni vsota. Tu boste ustvarili niz celih števil in poklicali svojo rekurzivno metodo.

2. korak: Ustvarite glavo rekurzivne metode

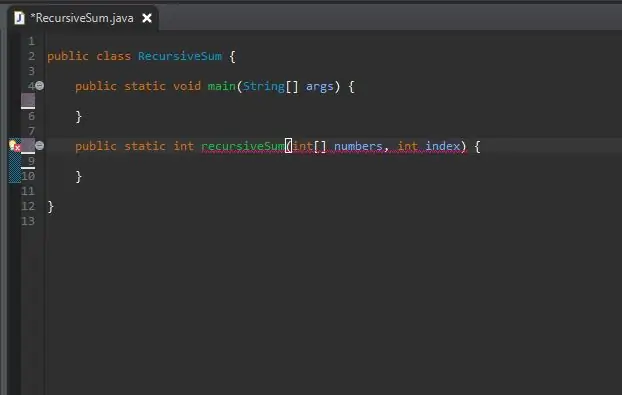
Zunaj glavne metode ustvarite glavo metode za svojo rekurzivno metodo.

Metoda je statična, saj za njeno uporabo ne bo potreben predmet.

Vrnjeni tip je int, saj bo polje, ki ga bomo uporabljali, polno na cela števila. To pa lahko spremenite v katero koli vrsto številke, ki jo vsebuje matrika.

Svojo metodo sem poimenoval recursiveSum, ki bo sprejela dva parametra; niz celih števil in indeks, ki ga bomo seštevku dodali. Te parametre sem poimenoval številke oziroma indeks.

Takoj boste videli napake in to je v redu. Kasneje bodo popravljeni.

3. korak: Ustvarite svojo torbico/osnovno torbico

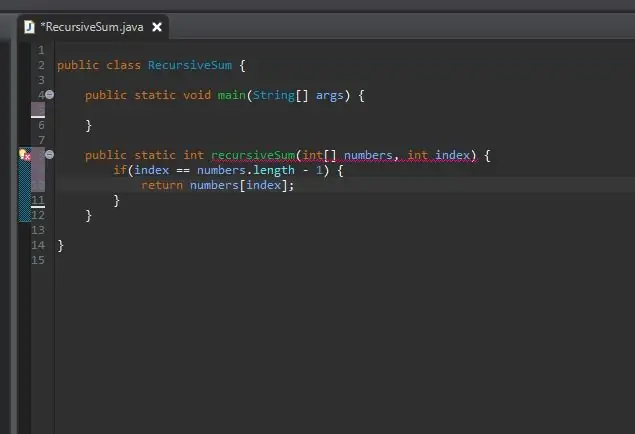
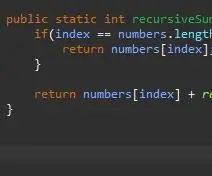
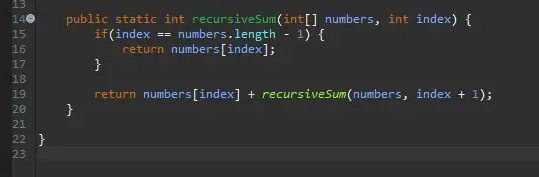
Rekurzivna metoda potrebuje začetni/osnovni primer. To je pogoj, zaradi katerega se vaša metoda ne bo neskončno klicala. Ta osnovni primer je lahko najpreprostejši primer, s katerim se bomo srečali. V tem primeru bo osnovni primer, ko smo na koncu matrike. Če je trenutni indeks enak dolžini matrike (minus 1, ker se matrike začnejo šteti od 0, ne 1), smo na koncu in ta element preprosto vrnemo pri tem indeksu.

4. korak: rekurzivni korak

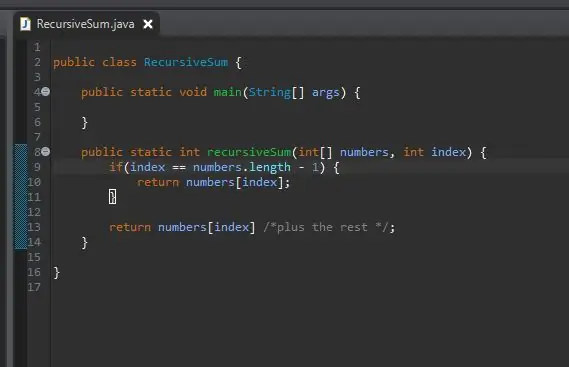
Ko imamo osnovni primer, je naslednji korak naš rekurzivni korak. Tu se zgodi čarovnija. Obravnavali smo primer, ko je naš indeks enak zadnjemu elementu v našem nizu. Kaj pa, če nismo zadnji element v svojem nizu? Kaj pa, če bi mu preprosto povedali, naj doda naš trenutni element in naslednjega? Sčasoma bomo dosegli konec našega niza in naš osnovni primer bo vplival.

Da bi to dosegli, preprosto vrnemo naš trenutni indeks in "dodamo preostanek" matrike.

5. korak: Skrajšajte težavo

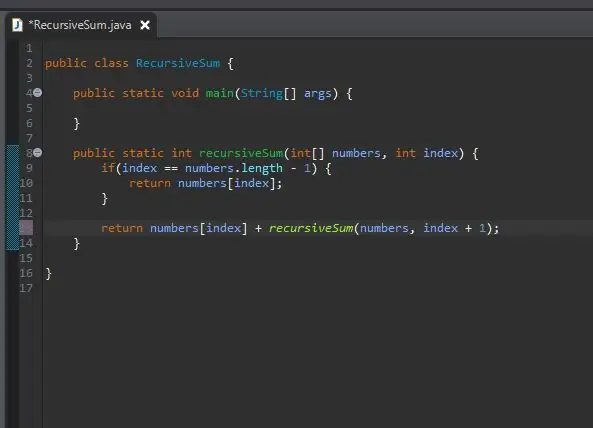
Kako preprosto "dodamo ostalo"? Že imamo metodo, ki bo dodala določen element; naša metoda rekurzivneSum ()! Lahko ga ponovno pokličemo, vendar spremenimo, kateri indeks seštevamo.

Prenesemo v isto matriko, ki jo obdelujemo, vendar posredujemo naslednji indeks iz našega trenutnega indeksa. To naredimo tako, da preprosto dodamo eno k našemu trenutnemu indeksu, kot je prikazano.

6. korak: Ustvarite niz celih števil

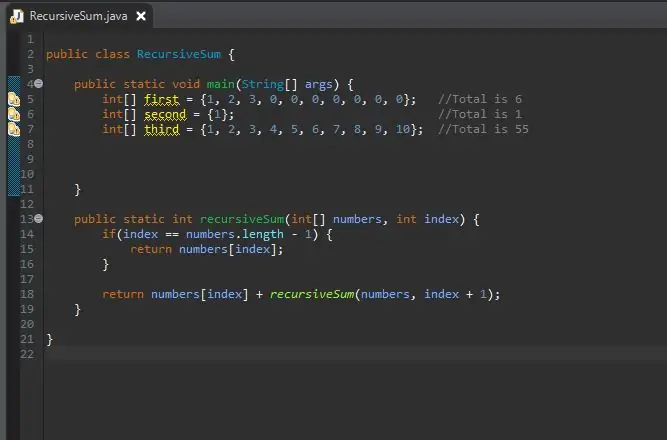
Zdaj, ko je naša metoda rekurzivnega seštevanja končana, lahko ustvarimo naš niz, ki ga bomo obdelali. Ta matrika bo v našem glavnem bloku metod.

Velikost matrike lahko nastavite tako dolgo, kot želite. Ustvaril sem nekaj različnih nizov z različnimi velikostmi in vrednostmi, ki dokazujejo, da deluje ne le v eni velikosti.

7. korak: Metodo pokličite s svojimi nizi

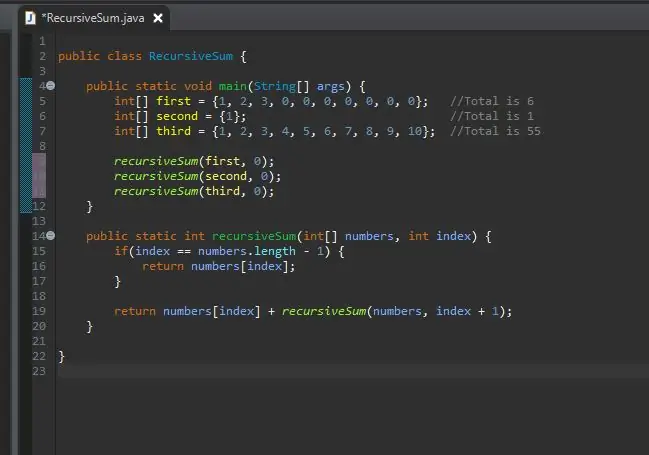
Zdaj lahko pokličete svojo rekurzivno metodo in ji posredujete te matrike. Zdaj lahko zaženete svoj program.

8. korak: Natisnite rezultate

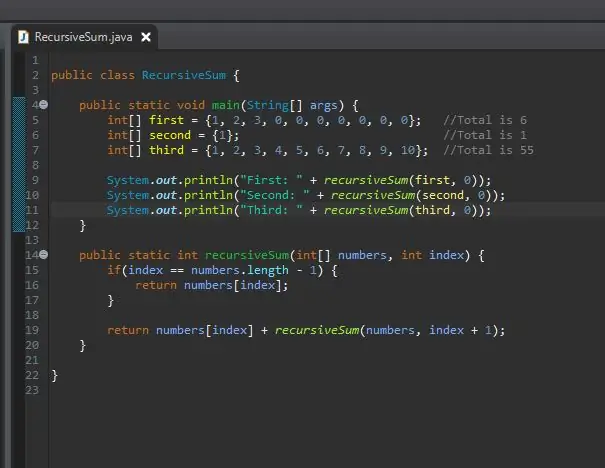
Se ni nič zgodilo. Zakaj? Rekurzivna vsota vrne celo število, vendar s tem celim številom nismo storili ničesar. Svoje je opravilo, rezultatov pa ne vidimo. Če si želite ogledati rezultat, ga preprosto natisnemo. Ko zaženete to, bi morali videti rezultate za vsak vaš niz.

9. korak: Čestitamo

Dokončali ste rekurzivno funkcijo. Spreminjajte velikost svojih nizov. Če ga preizkusite, boste opazili, da se zruši, ko imate prazno polje. Tega nismo upoštevali, vendar je to odličen način za izboljšanje vaše rekurzivne metode.