
Kazalo:
- Avtor John Day day@howwhatproduce.com.
- Public 2024-01-30 12:07.
- Nazadnje spremenjeno 2025-01-23 15:09.



V tem navodilu vam bom pokazal, kako z uporabo Arduina sestaviti igro Tic Tac Toe z umetno inteligenco. Lahko igrate proti Arduinu ali pa gledate, kako igra Arduino proti sebi.
Uporabljam algoritem, imenovan "minimaksni algoritem", ki ga lahko uporabimo ne le za izdelavo AI za Tic Tac Toe, ampak tudi za različne druge igre, kot so Four in a Row, dame ali celo šah. Igre, kot je šah, so zelo zapletene in zahtevajo veliko bolj izpopolnjene različice algoritma. Za našo igro Tic Tac Toe lahko uporabimo najpreprostejšo različico algoritma, ki je kljub temu precej impresivna. Pravzaprav je AI tako dobra, da je nemogoče premagati Arduino!
Igro je enostavno sestaviti. Potrebujete le nekaj sestavin in skico, ki sem jo napisal. Dodal sem tudi podrobnejšo razlago algoritma, če želite razumeti, kako deluje.
1. korak: Zgradite in igrajte
Za izdelavo igre Tic Tac Toe potrebujete naslednje komponente:
- Arduino Uno
- 9 LED WS2812 RGB
- 9 gumbov
- nekaj žičnih in mostičnih kablov
Povežite komponente, kot je prikazano na skici Fritzing. Nato kodo naložite v svoj Arduino.
Arduino privzeto prvi zavije. Da bi bile stvari nekoliko bolj zanimive, je prva poteza izbrana naključno. Po prvi potezi Arduino uporablja algoritem minimaksa za določitev najboljše možne poteze. Novo igro začnete s ponastavitvijo Arduina.
Arduino lahko "razmišljate" tako, da odprete serijski monitor. Za vsako možno potezo algoritem izračuna oceno, ki kaže, ali bo ta premik pripeljal do zmage (vrednost 10) ali izgube (vrednost -10) za Arduino ali neodločenega rezultata (vrednost 0).
Arduino si lahko ogledate tudi proti samemu sebi, tako da na samem začetku skeča komentirate vrstico "#define DEMO_MODE". Če naložite spremenjeno skico, Arduino naredi prvi korak naključno in nato z algoritmom minimaksa določi najboljšo potezo za vsakega igralca v vsakem potezu.
Upoštevajte, da proti Arduinu ne morete zmagati. Vsaka tekma se konča z neodločenim izidom ali pa izgubite, če naredite napako. To je zato, ker algoritem vedno izbere najboljšo možno potezo. Kot morda veste, se igra Tic Tac Toe vedno konča neodločeno, če oba igralca ne naredita napake. V demo načinu se vsaka igra konča neodločeno, saj, kot vsi vemo, računalniki nikoli ne delajo napak;-)
2. korak: Minimaksni algoritem

Algoritem je sestavljen iz dveh komponent: funkcije ocenjevanja in strategije iskanja. Ocenjevalna funkcija je funkcija, ki dodeli numerično vrednost položajem plošče. Če je položaj končni položaj (tj. Položaj, kjer je zmagal modri ali rdeči igralec ali kjer nobeden od njih ni zmagal), je funkcija ocenjevanja zelo preprosta: recimo, da Arduino igra modro, človeški igralec pa rdeče. Če je položaj zmagovalni položaj za modro, funkcija temu položaju dodeli vrednost 10; če je zmagovalni položaj za rdečo, funkcija dodeli poziciji vrednost -10; in če je položaj neodločen, funkcija dodeli vrednost 0.
Ko je na vrsti Arduino, želi izbrati potezo, ki maksimira vrednost funkcije ocenjevanja, saj maksimiziranje vrednosti pomeni, da bo raje zmagal nad neodločenim izidom (10 je več kot 0) in omogočil neodločen rezultat nad izgubo (0 je večji od -10). S podobnim argumentom želi nasprotnica igrati tako, da zmanjša vrednost ocenjevalne funkcije.
Za nedokončno pozicijo algoritem izračuna vrednost funkcije vrednotenja s pomočjo rekurzivne strategije iskanja. Od trenutnega položaja izmenično simulira vse poteze, ki jih lahko izvedeta modri in rdeči igralec. To je mogoče prikazati kot drevo, kot je prikazano na diagramu. Ko pride na končni položaj, se začne umakniti in vrednost vrednosti vrednotenja prenese z nižje ravni rekurzije na višjo raven rekurzije. Dodeljuje največ (če je v ustreznem koraku rekurzije na vrsti modri igralec) ali najmanjšo vrednost (če je v ustreznem koraku rekurzije na vrsti rdeči igralec) vrednosti funkcije ocenjevanja od spodnje ravni rekurzije do položaja na višja stopnja rekurzije. Nazadnje, ko je algoritem končal korak nazaj in spet prišel na trenutni položaj, je potreben tisti premik (ali eden od potezov), ki ima največjo vrednost funkcije vrednotenja.
Morda se to sliši nekoliko abstraktno, v resnici pa ni tako težko. Razmislite o položaju, prikazanem na vrhu diagrama. V prvem koraku rekurzije lahko modro naredite tri različne poteze. Modra poskuša povečati vrednost ocenjevalne funkcije. Za vsako potezo, ki jo lahko izvede modra, obstajata dve potezi, ki jo lahko naredi rdeča. Rdeča poskuša minimizirati vrednost funkcije vrednotenja. Razmislite o potezi, kjer igra modra v zgornjem desnem kotu. Če rdeča igra v osrednjem polju, je rdeča zmagala (-10). Če pa rdeča igra v spodnjem okvirju na sredini, bo modra zmagala v naslednji potezi (10). Če se torej v zgornjem desnem kotu igra modra, se bo v osrednjem polju predvajala rdeča, saj s tem minimizira vrednost funkcije ocenjevanja. Podobno, če se v osrednjem spodnjem polju predvaja modra, se bo v osrednjem polju spet predvajala rdeča, ker to minimizira funkcijo ocenjevanja. Če na drugi strani modra igra v osrednjem polju, ni pomembno, katero potezo vzame rdeča, modra bo vedno zmagala (10). Ker želi modra maksimizirati funkcijo vrednotenja, se bo predvajala v osrednjem polju, saj ima ta položaj večjo vrednost funkcije ocenjevanja (10) kot drugi dve potezi (-10).
3. korak: Odpravljanje težav in nadaljnji koraki
Če pritisnete gumb in zasveti drugačna LED od tiste, ki ustreza gumbu, ste najverjetneje pomešali žice na nožicah A0-A2 ali 4-6 ali pa ste LED priključili v napačnem vrstnem redu.
Upoštevajte tudi, da algoritem ne izbere vedno poteze, ki bo Arduinu omogočila čim hitrejšo zmago. Pravzaprav sem nekaj časa odpravljal napake v algoritmu, ker Arduino ni izbral poteze, ki bi bila zmagovalna. Trajalo je nekaj časa, dokler nisem spoznal, da je namesto tega izbral potezo, ki je zagotovila, da bo zmagal eno potezo kasneje. Če želite, lahko poskusite spremeniti algoritem, tako da bo vedno imel prednost zmagovalno potezo pred poznejšo zmago.
Možna razširitev tega projekta bi bila uporaba algoritma za izdelavo AI za 4x4 ali celo 5x5 Tic Tac Toe. Upoštevajte pa, da se število položajev, ki jih mora algoritem pregledati, zelo hitro povečuje. Morali boste najti načine, kako narediti ocenjevalno funkcijo bolj inteligentno, tako da dodelite vrednosti položajem, ki niso dokončni, glede na verjetnost, da je položaj dober ali slab za zadevnega igralca. Iskanje bi lahko poskušali narediti tudi bolj inteligentno, tako da predčasno ustavite rekurzijo, če se izkaže, da je poteza manj vredna nadaljnjega raziskovanja kot alternativne poteze.
Arduino zaradi omejenega pomnilnika verjetno ni najboljša platforma za takšne razširitve. Rekurzija omogoča, da se sklad med izvajanjem programa poveča, in če se sklad preveč poveča, lahko poškoduje programski pomnilnik, kar povzroči zrušitve ali neredno vedenje. Za ta projekt sem se odločil predvsem zato, ker sem hotel preveriti, ali je to mogoče in v izobraževalne namene, ne pa zato, ker je to najboljša izbira za tovrstne težave.
Priporočena:
Igra Python Tic Tac Toe: 4 koraki

Python Tic Tac Toe Game: igra python tic tac toe ta igra je narejena v pythonu, ki je računalniški jezik, uporabil sem urejevalnik python, imenovan: pycharm, lahko uporabite tudi običajen urejevalnik kode python
Samoizravnalni robot - PID nadzorni algoritem: 3 koraki

Self Balancing Robot - PID Control Algorithm: Ta projekt je bil zasnovan, ker me je zanimalo, da bi izvedeli več o nadzornih algoritmih in kako učinkovito implementirati funkcionalne zanke PID. Projekt je še v fazi razvoja, saj bo modul Bluetooth še dodan, kar bo
Kordični algoritem z uporabo VHDL: 4 koraki
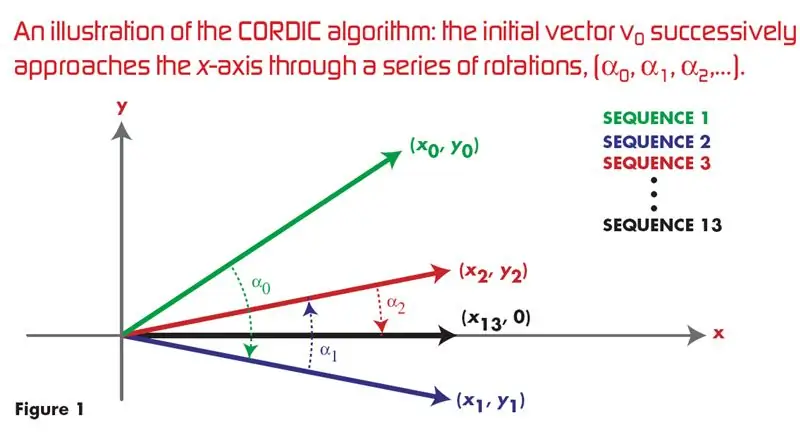
Kordični algoritem z uporabo VHDL: ## To je najbolj priljubljena in priljubljena povezava v Googlu za VHDL implementacijo CORDIC ALGORITMA za ustvarjanje sinusnega in kosinusnega vala ## Trenutno obstaja veliko strojno učinkovitih algoritmov, vendar ti niso znani zaradi prevlada softwarja
Umetna inteligenca družabnih iger: minimalni algoritem: 8 korakov
Umetna inteligenca družabnih iger: algoritem minimaksa: Ste se kdaj vprašali, kako so narejeni računalniki, s katerimi igrate v šahu ali šahu? No, ne glejte dlje od tega navodila, saj vam bo pokazalo, kako narediti preprosto, a učinkovito umetno inteligenco (AI) z algoritmom minimaksa! Z uporabo th
Igra Microbit Tic Tac Toe: 4 koraki (s slikami)

Igra Microcit Tic Tac Toe: Za ta projekt sva s sodelavcem - @descartez ustvarila odlično igro tac tae z uporabo radijske funkcije mikrobitov. Če še niste slišali za mikrobite, so odličen mikrokrmilnik, namenjen učenju otrok programiranja. Oni
