
Kazalo:
- Avtor John Day day@howwhatproduce.com.
- Public 2024-01-30 12:10.
- Nazadnje spremenjeno 2025-01-23 15:10.
Uvod
Ta priročnik je namenjen vsem, ki jih zanima uporaba merilnikov pospeška in žiroskopov ter kombiniranih naprav IMU (enota za inercialno merjenje) v njihovih projektih elektronike
Zajemali bomo:
- Kaj meri merilnik pospeška?
- Kaj meri žiroskop (znan tudi kot žiroskop)?
- Kako pretvoriti analogno-digitalne (ADC) odčitke, ki jih dobite s tega senzorja, v fizične enote (to bi bilo g za merilnik pospeška, deg/s za žiroskop)
- Kako združiti odčitke merilnika pospeška in žiroskopa, da dobite natančne informacije o naklonu vaše naprave glede na osnovno ravnino
V celotnem članku bom poskušal matematiko čim bolj omejiti. Če veste, kaj so sinus/kosinus/tangent, bi morali razumeti in uporabiti te zamisli v svojem projektu, ne glede na to, katero platformo uporabljate: Arduino, propeler, osnovni žig, čipi Atmel, mikročip PIC itd.
Obstajajo ljudje, ki menijo, da za uporabo enote IMU potrebujete kompleksno matematiko (kompleksni filtri FIR ali IIR, kot so Kalmanovi filtri, filtri Parks-McClellan itd.). Vse to lahko raziščete in dosežete čudovite, a kompleksne rezultate. Moj način razlage stvari zahteva le osnovno matematiko. Zelo verjamem v preprostost. Mislim, da je preprost sistem lažje nadzorovati in spremljati, poleg tega pa številne vgrajene naprave nimajo moči in sredstev za izvajanje kompleksnih algoritmov, ki zahtevajo matrične izračune.
Kot primer bom uporabil novo enoto IMU, merilnik pospeška Acc_Gyro + žiroskop IMU. V spodnjih primerih bomo uporabili parametre te naprave. Ta enota je dobra naprava za začetek, saj jo sestavljata 2 napravi:
- LIS331AL (podatkovni list) - triosni merilnik pospeška 2G - LPR550AL (podatkovni list) - dvoosni nagib in nagib, žiroskop 500 stopinj/s
Skupaj predstavljata enoto za inercialno merjenje 5 stopinj svobode. Zdaj je to čudovito ime! Kljub temu je za domišljijskim imenom zelo uporabna kombinirana naprava, ki jo bomo v tem priročniku podrobno opisali in razložili.
Korak: Merilnik pospeška
Za razumevanje te enote bomo začeli z merilnikom pospeška. Pri razmišljanju o merilcih pospeška je pogosto koristno prikazati polje v obliki kocke s kroglico v njej. Lahko si predstavljate kaj drugega, kot je piškotek ali krof, jaz pa si predstavljam kroglo:
Če vzamemo to škatlo na mesto brez gravitacijskih polj ali brez drugih polj, ki bi lahko vplivala na položaj žoge - bo žoga preprosto lebdela na sredini škatle. Lahko si predstavljate, da je škatla v vesolju, daleč stran od kakršnih koli kozmičnih teles, ali če je tak kraj težko najti, si predstavljajte vsaj vesoljsko plovilo, ki kroži okoli planeta, kjer je vse v breztežnem stanju. Na zgornji sliki lahko vidite, da vsaki osi dodelimo par sten (steno Y+ smo odstranili, da lahko pogledamo v okvir). Predstavljajte si, da je vsaka stena občutljiva na pritisk. Če nenadoma premaknemo polje v levo (pospešimo ga s pospeškom 1g = 9,8m/s^2), bo žoga udarila v steno X-. Nato izmerimo tlačno silo, ki jo krogla deluje na steno, in na os X iznese vrednost -1g.
Upoštevajte, da bo merilnik pospeška dejansko zaznal silo, ki je usmerjena v nasprotni smeri od vektorja pospeška. Ta sila se pogosto imenuje inercialna sila ali fiktivna sila. Iz tega se morate naučiti, da merilnik pospeška posredno meri pospešek s silo, ki deluje na eno od njegovih sten (po našem modelu je to lahko vzmet ali kaj drugega v merilcih pospeška v resničnem življenju). To silo lahko povzroči pospešek, vendar, kot bomo videli v naslednjem primeru, ni vedno posledica pospeška.
Če vzamemo naš model in ga postavimo na Zemljo, bo žoga padla na Z-steno in na spodnjo steno uporabila silo 1 g, kot je prikazano na spodnji sliki:
V tem primeru se polje ne premika, vendar še vedno dobimo odčitek -1g na osi Z. Tlak, ki ga je krogla pritisnila na steno, je povzročila gravitacijska sila. V teoriji bi to lahko bila druga vrsta sile - na primer, če si predstavljate, da je naša žoga kovinska, bi lahko magnet ob škatli premaknil, tako da udari v drugo steno. To je bilo rečeno samo zato, da bi dokazali, da merilnik pospeška v bistvu ne meri pospeška. Zgodi se, da pospešek povzroči vztrajnostno silo, ki jo zajame mehanizem zaznavanja sile merilnika pospeška.
Čeprav ta model ni ravno konstruiran senzor MEMS, je pogosto uporaben pri reševanju težav, povezanih s merilnikom pospeška. Pravzaprav obstajajo podobni senzorji, ki imajo v notranjosti kovinske kroglice, imenujemo jih stikala za nagib, vendar so bolj primitivna in običajno lahko povedo le, ali je naprava nagnjena v nekem območju ali ne, ne pa tudi obsega nagiba.
Doslej smo analizirali izhod merilnika pospeška na eni osi in to je vse, kar boste dobili z enoosnimi merilniki pospeška. Dejanska vrednost triosnih merilnikov pospeška izhaja iz dejstva, da lahko zaznajo vztrajnostne sile na vseh treh osh. Vrnimo se k modelu škatle in zavrtimo polje za 45 stopinj v desno. Žoga se bo zdaj dotaknila dveh sten: Z- in X-, kot je prikazano na spodnji sliki:
Vrednosti 0,71 niso poljubne, dejansko so približek za SQRT (1/2). To bo postalo bolj jasno, ko predstavimo naslednji model merilnika pospeška.
V prejšnjem modelu smo fiksirali gravitacijsko silo in zasukali našo namišljeno škatlo. V zadnjih 2 primerih smo analizirali izhod v dveh različnih položajih škatle, medtem ko je vektor sile ostal konstanten. Čeprav je bilo to koristno pri razumevanju, kako merilnik pospeška deluje z zunanjimi silami, je bolj praktično izvesti izračune, če koordinatni sistem pritrdimo na osi merilnika pospeška in si predstavljamo, da se vektor sile vrti okoli nas.
Oglejte si zgornji model, ohranil sem barve osi, da lahko miselno preidete iz prejšnjega modela v novega. Predstavljajte si, da je vsaka os v novem modelu pravokotna na ustrezne ploskve škatle v prejšnjem modelu. Vektor R je vektor sile, ki ga meri merilnik pospeška (lahko je to gravitacijska sila ali inercialna sila iz zgornjih primerov ali kombinacija obeh). Rx, Ry, Rz so projekcija vektorja R na osi X, Y, Z. Upoštevajte naslednje razmerje:
R^2 = Rx^2 + Ry^2 + Rz^2 (enačba 1)
ki je v bistvu enakovreden Pitagorinemu izreku v 3D.
Ne pozabite, da sem vam malo prej povedal, da vrednosti SQRT (1/2) ~ 0,71 niso naključne. Če jih vključite v zgornjo formulo, potem ko se spomnimo, da je bila naša gravitacijska sila 1 g, lahko preverimo, da:
1^2 = (-SQRT (1/2))^2 + 0^2 + (-SQRT (1/2))^2
preprosto z zamenjavo R = 1, Rx = -SQRT (1/2), Ry = 0, Rz = -SQRT (1/2) v enačbi 1
Po dolgi preambuli teorije se približujemo merilnikom pospeška v resničnem življenju. Vrednosti Rx, Ry, Rz so dejansko linearno povezane z vrednostmi, ki jih bo prikazal vaš merilnik pospeška v resničnem življenju in ki jih lahko uporabite za izvajanje različnih izračunov.
Preden pridemo tja, se pogovorimo malo o tem, kako nam merilniki pospeška posredujejo te podatke. Večina merilnikov pospeška bo razdeljena v dve kategoriji: digitalne in analogne. Digitalni merilniki pospeška vam bodo dali informacije z uporabo serijskega protokola, kot sta I2C, SPI ali USART, medtem ko bodo analogni merilniki pospeška izpisali napetost v vnaprej določenem območju, ki ga morate pretvoriti v digitalno vrednost z modulom ADC (analogno -digitalni pretvornik). Ne bom se spuščal v podrobnosti o tem, kako deluje ADC, deloma zato, ker je tako obsežna tema, deloma pa zato, ker se razlikuje od platforme do platforme. Nekateri mikrokrmilniki bodo imeli vgrajene module ADC, nekateri bodo potrebovali zunanje komponente za izvedbo pretvorb ADC. Ne glede na vrsto modula ADC, ki ga uporabljate, boste dobili vrednost v določenem območju. Na primer 10 -bitni ADC modul bo izpisal vrednost v območju 0..1023, upoštevajte, da je 1023 = 2^10 -1. 12-bitni ADC modul bo izpisal vrednost v območju 0..4095, upoštevajte, da je 4095 = 2^12-1.
Nadaljujmo s preprostim primerom, recimo, da nam je naš 10 -bitni ADC modul dal naslednje vrednosti za tri kanale merilnika pospeška (osi):
AdcRx = 586 AdcRy = 630 AdcRz = 561
Vsak modul ADC bo imel referenčno napetost, v našem primeru predpostavimo, da je 3.3V. Za pretvorbo 10 -bitne vrednosti adc v napetost uporabimo naslednjo formulo:
VoltsRx = AdcRx * Vref / 1023
Na kratko tukaj: za 8 -bitni ADC bi bil zadnji delilec 255 = 2 ^ 8 -1, za 12 -bitni ADC pa bi bil zadnji delilec 4095 = 2 ^ 12 -1.
Če uporabimo to formulo za vse 3 kanale, dobimo:
VoltsRx = 586 * 3.3V / 1023 = ~ 1.89V (vse rezultate zaokrožimo na 2 decimalni mesti) VoltsRy = 630 * 3.3V / 1023 = ~ 2.03V VoltsRz = 561 * 3.3V / 1023 = ~ 1.81V
Vsak merilnik pospeška ima napetostni nivo nič g, najdete ga v specifikacijah, to je napetost, ki ustreza 0 g. Za pridobitev podpisane vrednosti napetosti moramo izračunati premik s te ravni. Recimo, da je naša napetost 0 g VzeroG = 1,65 V. Premike napetosti od napetosti nič g izračunamo na naslednji način:
DeltaVoltsRx = 1.89V - 1.65V = 0.24V DeltaVoltsRy = 2.03V - 1.65V = 0.38V DeltaVoltsRz = 1.81V - 1.65V = 0.16V
Zdaj imamo odčitke merilnika pospeška v voltih, še vedno ni v g (9,8 m/s^2), za končno pretvorbo uporabimo občutljivost merilnika pospeška, običajno izraženo v mV/g. Recimo, da je naša občutljivost = 478,5 mV/g = 0,4785 V/g. Vrednosti občutljivosti najdete v specifikacijah merilnika pospeška. Za izračun končnih sil, izraženih v g, uporabimo naslednjo formulo:
Rx = DeltaVoltsRx / Občutljivost
Rx = 0,24 V / 0,4785 V / g = ~ 0,5 g Ry = 0,38 V / 0,4785 V / g = ~ 0,79 g Rz = 0,16 V / 0,4785 V / g = ~ 0,33 g
Seveda bi lahko vse korake združili v eno formulo, vendar sem šel skozi vse korake, da bi bilo jasno, kako greš od odčitkov ADC do komponente vektorja sile, izražene v g.
Rx = (AdcRx * Vref / 1023 - VzeroG) / Občutljivost (Eq.2) Ry = (AdcRy * Vref / 1023 - VzeroG) / Občutljivost Rz = (AdcRz * Vref / 1023 - VzeroG) / Občutljivost
Zdaj imamo vse 3 komponente, ki določajo naš vektor vztrajnostne sile, če na napravo ne vplivajo druge sile razen gravitacije, lahko domnevamo, da je to smer našega vektorja gravitacijske sile. Če želite izračunati naklon naprave glede na tla, lahko izračunate kot med tem vektorjem in osjo Z. Če vas zanima tudi smer nagiba na os, lahko ta rezultat razdelite na 2 komponenti: naklon na osi X in Y, ki se lahko izračuna kot kot med gravitacijskim vektorjem in osmi X / Y. Izračun teh kotov je bolj preprost, kot si mislite, zdaj ko smo izračunali vrednosti za Rx, Ry in Rz. Vrnimo se k zadnjemu modelu merilnika pospeška in naredimo nekaj dodatnih zapisov:
Koti, ki nas zanimajo, so koti med osmi X, Y, Z in vektorjem sile R. Te kote bomo opredelili kot Axr, Ayr, Azr. Iz pravokotnega trikotnika, ki ga tvorita R in Rx, lahko opazite, da:
cos (Axr) = Rx / R in podobno: cos (Ayr) = Ry / R cos (Azr) = Rz / R
Iz enačbe 1 lahko sklepamo, da je R = SQRT (Rx^2 + Ry^2 + Rz^2).
Svoje kote lahko zdaj najdemo z uporabo funkcije arccos () (inverzna funkcija cos ()):
Axr = arccos (Rx/R) Ayr = arccos (Ry/R) Azr = arccos (Rz/R)
Razlagali smo model merilnika pospeška, da bi prišli do teh formul. Glede na vaše aplikacije boste morda želeli uporabiti vmesne formule, ki smo jih izpeljali. Kmalu bomo predstavili tudi model žiroskopa in videli bomo, kako lahko podatke pospeška in žiroskopa združimo, da zagotovimo še natančnejše ocene naklona.
Toda preden to storimo, naredimo še nekaj uporabnih zapisov:
cosX = cos (Axr) = Rx / R cozy = cos (Ayr) = Ry / R cosZ = cos (Azr) = Rz / R
Ta trojka se pogosto imenuje smerni kosinus in v bistvu predstavlja vektor enote (vektor z dolžino 1), ki ima isto smer kot naš vektor R. Z lahkoto lahko preverite, da:
SQRT (cosX^2 + udobno^2 + cosZ^2) = 1
To je lepa lastnost, saj nas oprošča spremljanja modula (dolžine) vektorja R. Pogosto, če nas samo zanima smer našega inercialnega vektorja, je smiselno normalizirati njegov modul, da poenostavimo druge izračune.
2. korak: žiroskop
Za žiroskop ne bomo predstavili nobenega enakovrednega modela škatle, kot smo to storili za merilnik pospeška, namesto tega bomo skočili naravnost na drugi model merilnika pospeška in pokazali bomo, kaj meri žiroskop po tem modelu.
Vsak kanal žiroskopa meri vrtenje okoli ene od osi. Na primer, dvoosni žiroskop bo meril vrtenje okoli osi X in Y (ali nekateri lahko rečejo "približno"). Za izražanje te rotacije v številkah naredimo nekaj zapisov. Najprej opredelimo:
Rxz - je projekcija vektorja vztrajnostne sile R na ravnino XZ Ryz - je projekcija vektorja vztrajnostne sile R na ravnino YZ
Iz pravokotnega trikotnika, ki ga tvorita Rxz in Rz, s pomočjo Pitagorjevega izreka dobimo:
Rxz^2 = Rx^2 + Rz^2 in podobno: Ryz^2 = Ry^2 + Rz^2
upoštevajte tudi:
R^2 = Rxz^2 + Ry^2, to lahko izpeljemo iz enačbe 1 in zgoraj, ali pa iz pravokotnega trikotnika, ki ga tvorita R in Ryz R^2 = Ryz^2 + Rx^2
V tem članku teh formul ne bomo uporabljali, vendar je koristno opozoriti na povezavo med vsemi vrednostmi v našem modelu.
Namesto tega bomo definirali kot med osjo Z in vektorji Ryx, Ryz, kot sledi:
Axz - je kot med Rxz (projekcija R na ravnino XZ) in osjo Ayz - je kot med Ryz (projekcija R na ravnino YZ) in osjo Z
Zdaj smo vse bližje meritvam žiroskopa. Žiroskop meri hitrost sprememb zgoraj definiranih kotov. Z drugimi besedami, izpisal bo vrednost, ki je linearno povezana s hitrostjo spreminjanja teh kotov. Za razlago tega predpostavimo, da smo v času t0 izmerili kot vrtenja okoli osi Y (to bi bil kot Axz) in ga definiramo kot Axz0, nato smo ta kot merili pozneje t1 in je bil Axz1. Stopnja spremembe se izračuna na naslednji način:
RateAxz = (Axz1 - Axz0) / (t1 - t0).
Če izrazimo Axz v stopinjah in čas v sekundah, bo ta vrednost izražena v stopinjah/s. To meri žiroskop.
V praksi vam žiroskop (razen če je poseben digitalni žiroskop) le redko da vrednost, izraženo v stopinjah/s. Enako kot za merilnik pospeška boste dobili vrednost ADC, ki jo boste morali pretvoriti v stopinje/s po formuli, podobni enačbi. 2, ki smo ga določili za merilnik pospeška. Predstavimo ADC v pretvorbeno formulo deg/s za žiroskop (predpostavljamo, da uporabljamo 10 -bitni ADC modul, za 8 -bitni ADC zamenjamo 1023 s 255, za 12 -bitni ADC zamenjamo 1023 s 4095).
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / Občutljivost Eq.3 RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / Občutljivost
AdcGyroXZ, AdcGyroYZ - dobimo iz našega modula adc in predstavljajo kanale, ki merijo vrtenje projekcije vektorja R v XZ v ravninah YZ, kar je ekvivalent, če rečemo, da je bilo vrtenje okoli osi Y oziroma X.
Vref - je referenčna napetost ADC, ki jo bomo uporabili 3,3 V v spodnjem primeru VzeroRate - je ničelna napetost, z drugimi besedami napetost, ki jo žiroskop odda, ko ni podvržen nobenemu vrtenju, za ploščo Acc_Gyro je na primer 1,23 V (te vrednosti najdete v specifikacijah) Občutljivost - če je občutljivost vašega žiroskopa izražena v mV / (deg / s), pogosto zapisana kot mV / deg / s, vam v bistvu pove, koliko mV bo povečanje izhoda žiroskopa, če povečate hitrost vrtenja za eno stopinjo/s. Občutljivost plošče Acc_Gyro je na primer 2mV/deg/s ali 0,002V/deg/s
Vzemimo primer, recimo, da je naš modul ADC vrnil naslednje vrednosti:
AdcGyroXZ = 571 AdcGyroXZ = 323
Z uporabo zgornje formule in parametrih specifikacij plošče Acc_Gyro dobimo:
RateAxz = (571 * 3,3 V/1023 - 1,23 V)/(0,002 V/deg/s) = ~ 306 stopinj/s RateAyz = (323 * 3,3 V/1023 - 1,23 V)/(0,002 V/deg/s) = ~ -94 stopinj/s
Z drugimi besedami, naprava se vrti okoli osi Y (ali lahko rečemo, da se vrti v ravnini XZ) s hitrostjo 306 stopinj/s in okoli osi X (ali lahko rečemo, da se vrti v ravnini YZ) s hitrostjo - 94 stopinj/s. Upoštevajte, da negativni znak pomeni, da se naprava vrti v nasprotni smeri od običajne pozitivne smeri. Ena smer vrtenja je po dogovoru pozitivna. Dober list s specifikacijami žiroskopa vam bo pokazal, katera smer je pozitivna, sicer jo boste morali poiskati tako, da poskusite z napravo in ugotovite, v katero smer vrtenja se poveča napetost na izhodnem zatiču. To je najbolje narediti z osciloskopom, saj se napetost takoj, ko ustavite vrtenje, spusti na ničelno raven. Če uporabljate multimeter, bi morali vsaj nekaj sekund vzdrževati konstantno hitrost vrtenja in pri tem zabeležiti napetost, nato pa jo primerjati z ničelno napetostjo. Če je večja od ničelne napetosti, pomeni, da je smer vrtenja pozitivna.
3. korak: Kombinacija merilnika pospeška in žiroskopa
Vse skupaj - Združevanje merilnikov pospeška in žiroskopa
Če berete ta članek, ste verjetno kupili ali nameravate kupiti napravo IMU ali pa jo nameravate zgraditi iz ločenih merilnikov pospeška in žiroskopa.
Prvi korak pri uporabi kombinirane naprave IMU, ki združuje merilnik pospeška in žiroskop, je poravnava njihovih koordinatnih sistemov. Najlažji način za to je, da kot referenčni koordinatni sistem izberete koordinatni sistem merilnika pospeška. Večina podatkovnih listov merilnika pospeška bo prikazala smer osi X, Y, Z glede na sliko fizičnega čipa ali naprave. Tu so na primer smeri osi X, Y, Z, kot je prikazano v specifikacijah za ploščo Acc_Gyro:
Naslednji koraki so:
Določite izhode žiroskopa, ki ustrezajo zgoraj obravnavanim vrednostim RateAxz, RateAyz. Ugotovite, ali je treba te izhode obrniti zaradi fizičnega položaja žiroskopa glede na merilnik pospeška
Ne predpostavljajte, da če ima žiroskop izhod z oznako X ali Y, bo ustrezal kateri koli osi v koordinatnem sistemu merilnika pospeška, tudi če je ta izhod del enote IMU. Najboljši način je, da ga preizkusite. Ob predpostavki, da ste fiksirali položaj žiroskopa glede na merilnik pospeška. Domneva se, da sta meji žiroskopa in merilnika pospeška vzporedni, kar pomeni, da žiroskop postavite pod kotom, večkratnim 90 stopinj glede na čip merilnika pospeška. Če ste kupili ploščo IMU, obstaja velika verjetnost, da so že usklajeni na ta način. V tem članku ne bomo razpravljali o modelih, pri katerih je žiroskop postavljen pod nepravilnim kotom glede na merilnik pospeška (recimo 45 ali 30 stopinj), čeprav je to v nekaterih aplikacijah lahko koristno.
Tukaj je vzorčno zaporedje za določitev, kateri izhod žiroskopa ustreza zgoraj obravnavani vrednosti RateAxz.
- napravo začnite postavljati v vodoravni položaj. Tako X kot Y izhodi merilnika pospeška bi oddajali ničelno napetost (na primer za ploščo Acc_Gyro je to 1,65 V)
- naslednjič začnite vrteti napravo okoli osi Y, drug način, da to rečete, je, da napravo zavrtite v ravnini XZ, tako da se izhoda merilnika pospeška X in Z spreminjata, izhod Y pa ostane konstanten. - med vrtenjem naprave s konstantno hitrostjo upoštevajte, kateri izhod žiroskopa se spreminja, morajo drugi izhodi žiroskopa ostati konstantni - izhod žiroskopa, ki se je spremenil med vrtenjem okoli osi Y (rotacija v ravnini XZ), bo zagotovil vhodno vrednost za AdcGyroXZ, iz katere izračunamo RateAxz - zadnji korak je zagotoviti, da smer vrtenja ustreza našemu modelu, v nekaterih primerih boste morda morali obrniti vrednost RateAxz zaradi fizičnega položaja žiroskopa glede na merilnik pospeška - znova izvedite zgornji preskus, pri čemer napravo obrnite okoli osi Y, tokrat spremljajte X izhod merilnika pospeška (AdcRx v našem modelu). Če AdcRx raste (prvih 90 stopinj vrtenja iz vodoravnega položaja), bi moral rasti tudi AdcGyroXZ. V nasprotnem primeru morate obrniti RateAxz, to lahko dosežete z uvedbo znakovnega faktorja v enačbi 3 na naslednji način:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / občutljivost, kjer je InvertAxz 1 ali -1
isti testni trs naredite za RateAyz, tako da napravo zavrtite okoli osi X, in ugotovite, kateri izhod žiroskopa ustreza RateAyz, in če ga je treba obrniti. Ko dobite vrednost za InvertAyz, uporabite naslednjo formulo za izračun RateAyza:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / občutljivost
Če bi naredili te teste na plošči Acc_Gyro, bi dobili naslednje rezultate:
- izhodni pin za RateAxz je GX4 in InvertAxz = -1. - izhodni pin za RateAyz je GY4 in InvertAyz = -1
Od tega trenutka dalje bomo šteli, da ste IMU nastavili tako, da lahko izračunate pravilne vrednosti za Axr, Ayr, Azr (kot je opredeljeno v 1. delu pospeška) in RateAxz, RateAyz (kot je opredeljeno v 2. delu žiroskopa).). Nato bomo analizirali razmerja med temi vrednostmi, ki se izkažejo za koristne za natančnejšo oceno naklona naprave glede na osnovno ravnino.
Morda se že sprašujete, če bi nam model merilnika pospeška že dal nagibne kote Axr, Ayr, Azr, zakaj bi se morali ukvarjati s podatki žiroskopa? Odgovor je preprost: podatkom merilnika pospeška ni mogoče vedno zaupati 100%. Razlogov je več, ne pozabite, da merilnik pospeška meri vztrajnostno silo, takšno silo lahko povzroči gravitacija (in v idealnem primeru le gravitacija), lahko pa tudi pospešek (premikanje) naprave. Posledično je merilnik pospeška, čeprav je v relativno stabilnem stanju, še vedno zelo občutljiv na vibracije in mehanski hrup na splošno. To je glavni razlog, zakaj večina sistemov IMU uporablja žiroskop za odpravo napak merilnika pospeška. Kako pa se to naredi? In ali je žiroskop brez hrupa?
Žiroskop ni brez hrupa, ker pa meri rotacijo, je manj občutljiv na linearna mehanska gibanja, vrsto hrupa, s katerim trpi merilnik pospeška, vendar imajo žiroskopi druge vrste težav, kot je na primer drift (ne vrača se na vrednost ničelne hitrosti) ko se vrtenje ustavi). Kljub temu lahko s povprečjem podatkov, ki prihajajo iz merilnika pospeška in žiroskopa, dobimo sorazmerno boljšo oceno trenutnega naklona naprave, kot bi jo dobili samo s podatki merilnika pospeška.
V naslednjih korakih bom predstavil algoritem, ki je bil navdihnjen z nekaterimi idejami, uporabljenimi v Kalmanovem filtru, vendar je veliko bolj enostaven in lažji za izvedbo na vgrajenih napravah. Pred tem poglejmo najprej, kaj želimo, da naš algoritem izračuna. No, vektor gravitacijske sile R = [Rx, Ry, Rz], iz katerega lahko izpeljemo druge vrednosti, kot so Axr, Ayr, Azr ali cosX, cozy, cosZ, nam bo dal idejo o naklonu naše naprave glede na osnovno ravnino razpravljamo o razmerju med temi vrednostmi v 1. delu. Lahko bi rekli - ali teh vrednosti Rx, Ry, Rz iz enačbe 2 v 1. delu že nimamo? No ja, vendar ne pozabite, da te vrednosti izhajajo samo iz podatkov merilnika pospeška, zato bi jih lahko uporabili neposredno v svoji aplikaciji, zato bi lahko dobili več hrupa, kot ga lahko prenese vaša aplikacija. Da bi se izognili nadaljnjim zmotam, ponovno opredelimo meritve merilnika pospeška na naslednji način:
Racc - je vektor vztrajnostne sile, merjen s merilnikom pospeška, ki je sestavljen iz naslednjih komponent (projekcije na osi X, Y, Z):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / Občutljivost RyAcc = (AdcRy * Vref / 1023 - VzeroG) / Občutljivost RzAcc = (AdcRz * Vref / 1023 - VzeroG) / Občutljivost
Doslej imamo nabor izmerjenih vrednosti, ki jih lahko pridobimo izključno iz vrednosti ADC merilnika pospeška. Temu nizu podatkov bomo rekli "vektor" in uporabili bomo naslednji zapis.
Racc = [RxAcc, RyAcc, RzAcc]
Ker je te komponente Racc mogoče dobiti iz podatkov merilnika pospeška, lahko to štejemo kot vhod v naš algoritem.
Upoštevajte, da boste, ker Racc meri silo gravitacije, pravilni, če predpostavite, da je dolžina tega vektorja, ki je opredeljena na naslednji način, enaka ali blizu 1 g.
| Racc | = SQRT (RxAcc^2 + RyAcc^2 + RzAcc^2), Vsekakor pa je smiselno ta vektor posodobiti na naslednji način:
Racc (normalizirano) = [RxAcc/| Racc |, RyAcc/| Racc |, RzAcc/| Racc |].
To bo zagotovilo, da je dolžina vašega normaliziranega vektorja Racc vedno 1.
Nato bomo predstavili nov vektor in ga poklicali
Počitek = [RxEst, RyEst, RzEst]
To bo rezultat našega algoritma, to so popravljene vrednosti, ki temeljijo na podatkih žiroskopa in na podlagi preteklih ocenjenih podatkov.
Naš algoritem bo naredil naslednje: - merilnik pospeška nam pove: "Zdaj ste na položaju Racc" - rečemo "Hvala, vendar naj preverim", - nato popravite te podatke s podatki žiroskopa, pa tudi s podatki o preteklih počitkih in oddamo nov ocenjeni vektor Rest. - menimo, da je počitek naša "najboljša stava" glede trenutnega položaja naprave.
Poglejmo, kako lahko to naredimo.
Začeli bomo z zaporedjem, če zaupamo merilniku pospeška in dodelimo:
Počitek (0) = Racc (0)
Mimogrede, spomnite se, da sta Rest in Racc vektorja, zato je zgornja enačba le preprost način za zapis 3 nizov enačb in se izognite ponavljanju:
RxEst (0) = RxAcc (0) RyEst (0) = RyAcc (0) RzEst (0) = RzAcc (0)
Nato bomo izvajali redne meritve v enakih časovnih presledkih T sekund in dobili bomo nove meritve, ki jih bomo opredelili kot Racc (1), Racc (2), Racc (3) itd. Nove ocene bomo izdali tudi v vsakem časovnem intervalu Počitek (1), Počitek (2), Počitek (3) itd.
Recimo, da smo na koraku n. Poznamo dva nabora vrednosti, ki bi jih radi uporabili:
Rest (n -1) - naša prejšnja ocena, z Rest (0) = Racc (0) Racc (n) - naša trenutna meritev merilnika pospeška
Preden lahko izračunamo Rest (n), uvedimo novo izmerjeno vrednost, ki jo lahko dobimo iz našega žiroskopa, in prejšnjo oceno.
Poimenovali ga bomo Rgyro in je tudi vektor, sestavljen iz treh komponent:
Rgyro = [RxGyro, RyGyro, RzGyro]
Ta vektor bomo izračunali po eno komponento naenkrat. Začeli bomo z RxGyro.
Začnimo z opazovanjem naslednje relacije v našem modelu žiroskopa, iz pravokotnega trikotnika, ki ga tvorita Rz in Rxz, lahko izpeljemo, da:
tan (Axz) = Rx/Rz => Axz = atan2 (Rx, Rz)
Atan2 je morda funkcija, ki je še niste uporabljali, podobna je atanu, le da vrne vrednosti v razponu (-PI, PI) v nasprotju s (-PI/2, PI/2), kot jo vrne atan, in potrebuje 2 argumenta namesto enega. Omogoča nam pretvorbo dveh vrednosti Rx, Rz v kote v celotnem območju 360 stopinj (-PI v PI). Več o atan2 si lahko preberete tukaj.
Tako poznamo RxEst (n-1) in RzEst (n-1), lahko najdemo:
Axz (n-1) = atan2 (RxEst (n-1), RzEst (n-1)).
Ne pozabite, da žiroskop meri hitrost spreminjanja kota Axz. Tako lahko novi kot Axz (n) ocenimo na naslednji način:
Axz (n) = Axz (n-1) + RateAxz (n) * T
Ne pozabite, da je RateAxz mogoče dobiti iz odčitkov ADC na žiroskopu. Natančnejša formula lahko uporabi povprečno hitrost vrtenja, izračunano na naslednji način:
RateAxzAvg = (RateAxz (n) + RateAxz (n-1)) / 2 Axz (n) = Axz (n-1) + RateAxzAvg * T
Na enak način najdemo:
Ayz (n) = Ayz (n-1) + RateAyz (n) * T
V redu, zdaj imamo Axz (n) in Ayz (n). Kam gremo od tu, da odštejemo RxGyro/RyGyro? Iz enačbe 1 lahko dolžino vektorja Rgyro zapišemo na naslednji način:
| Rgyro | = SQRT (RxGyro^2 + RyGyro^2 + RzGyro^2)
Tudi zato, ker smo normalizirali naš vektor Racc, lahko domnevamo, da je njegova dolžina 1 in se po rotaciji ni spremenila, zato je relativno varno zapisati:
| Rgyro | = 1
Za spodnje izračune sprejmemo začasen krajši zapis:
x = RxGyro, y = RyGyro, z = RzGyro
Z uporabo zgornjih razmerij lahko zapišemo:
x = x / 1 = x / SQRT (x^2+y^2+z^2)
Delimo števec in imenovalec ulomka na SQRT (x^2 + z^2)
x = (x / SQRT (x^2 + z^2)) / SQRT ((x^2 + y^2 + z^2) / (x^2 + z^2))
Upoštevajte, da je x / SQRT (x^2 + z^2) = sin (Axz), torej:
x = sin (Axz) / SQRT (1 + y^2 / (x^2 + z^2))
Zdaj pomnožite števec in imenovalec ulomka v SQRT z z^2
x = sin (Axz) / SQRT (1 + y^2 * z^2 / (z^2 * (x^2 + z^2)))
Upoštevajte, da je z / SQRT (x^2 + z^2) = cos (Axz) in y / z = tan (Ayz), zato na koncu:
x = sin (Axz) / SQRT (1 + cos (Axz)^2 * tan (Ayz)^2)
Če se vrnemo k zapisu, dobimo:
RxGyro = sin (Axz (n)) / SQRT (1 + cos (Axz (n))^2 * tan (Ayz (n))^2)
enako najdemo tudi mi
RyGyro = sin (Ayz (n)) / SQRT (1 + cos (Ayz (n))^2 * tan (Axz (n))^2)
Končno lahko najdemo:
RzGyro = Znak (RzGyro)*SQRT (1 - RxGyro^2 - RyGyro^2).
Kjer je Sign (RzGyro) = 1, ko je RzGyro> = 0, in Sign (RzGyro) = -1, ko je RzGyro <0.
Enostaven način za oceno tega je:
Znak (RzGyro) = Znak (RzEst (n-1))
V praksi bodite previdni, ko je RzEst (n-1) blizu 0. V tem primeru lahko celotno fazo žiroskopa preskočite in določite: Rgyro = Počitek (n-1). Rz se uporablja kot referenca za izračun kotov Axz in Ayz, in ko je blizu 0, se lahko vrednosti prelijejo in povzročijo slabe rezultate. Boste v domeni velikih številk s plavajočo vejico, kjer izvedba funkcije tan () / atan () morda ne bo natančna.
Torej povzemimo, kar imamo do zdaj, smo na koraku n našega algoritma in smo izračunali naslednje vrednosti:
Racc - trenutni odčitki našega merilnika pospeška Rgyro - pridobljeni iz počitka (n -1) in trenutnih odčitkov žiroskopa
Katere vrednosti uporabljamo za izračun posodobljene ocene Rest (n)? Verjetno ste uganili, da bomo uporabili oboje. Uporabili bomo tehtano povprečje, tako da:
Počitek (n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
To formulo lahko poenostavimo tako, da števec in imenovalec ulomka delimo z w1.
Počitek (n) = (Racc * w1/w1 + Rgyro * w2/w1)/(w1/w1 + w2/w1)
in po zamenjavi w2/w1 = wGyro dobimo:
Počitek (n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
Na zgornji forumu nam wGyro pove, koliko zaupamo svojemu žiroskopu v primerjavi s merilnikom pospeška. To vrednost lahko eksperimentalno izberete, običajno vrednosti med 5..20 sprožijo dobre rezultate.
Glavna razlika tega algoritma od Kalmanovega filtra je v tem, da je ta teža relativno fiksna, medtem ko se v Kalmanovem filteru uteži trajno posodobijo na podlagi izmerjenega hrupa odčitkov merilnika pospeška. Kalmanov filter je osredotočen na zagotavljanje "najboljših" teoretičnih rezultatov, medtem ko vam lahko ta algoritem daje rezultate "dovolj dobre" za vašo praktično uporabo. Lahko uporabite algoritem, ki wGyro prilagodi glede na nekatere faktorje hrupa, ki jih izmerite, vendar bodo fiksne vrednosti dobro delovale za večino aplikacij.
Še en korak nas loči od pridobivanja posodobljenih ocenjenih vrednosti:
RxEst (n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro) RyEst (n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro) RzEst (n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
Zdaj pa normalizirajmo ta vektor:
R = SQRT (RxEst (n)^2 + RyEst (n)^2 + RzEst (n)^2)
RxEst (n) = RxEst (n)/R RyEst (n) = RyEst (n)/R RzEst (n) = RzEst (n)/R
In spet smo pripravljeni ponoviti našo zanko.
Ta priročnik se je prvotno pojavil na starlino.com, naredil sem nekaj lahkih popravkov in ga z dovoljenjem ponovno objavil. Hvala Starlino!
Priporočena:
Raspberry Pi - ADXL345 3 -osni merilnik pospeška Python: 4 koraki

Raspberry Pi-ADXL345 3-osni merilnik pospeška Python: ADXL345 je majhen, tanek, 3-osni merilnik pospeška z ultra nizko močjo z visoko ločljivostjo (13-bitno) merjenjem do ± 16 g. Digitalni izhodni podatki so oblikovani kot 16-bitni dvojčki, ki se dopolnjujejo in so dostopni prek digitalnega vmesnika I2 C. Meri
Žiroskop MPU 6050, komunikacija merilnika pospeška z Arduinom (Atmega328p): 5 korakov
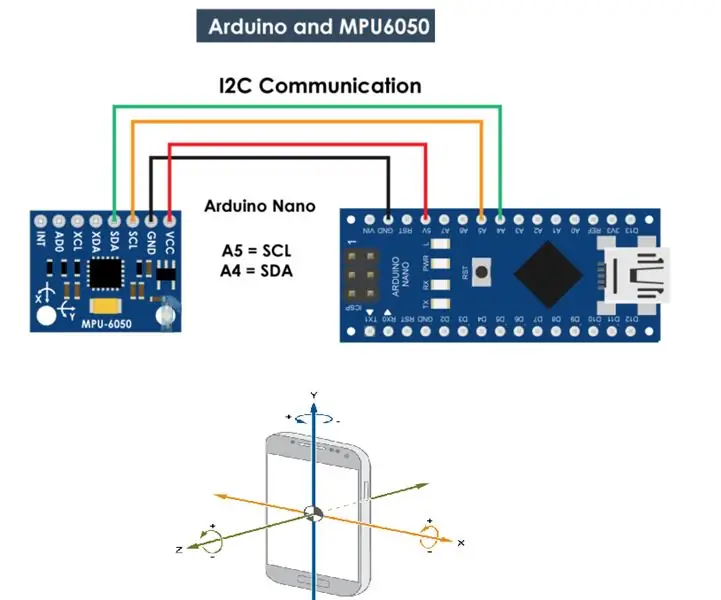
Žiroskop MPU 6050, komunikacija merilnika pospeška z Arduinom (Atmega328p): MPU6050 IMU ima 3-osni merilnik pospeška in 3-osni žiroskop, integriran na enem čipu. Žiroskop meri hitrost vrtenja ali hitrost spreminjanja kotnega položaja skozi čas, vzdolž Osi X, Y in Z. Izhodi žiroskopa so
Arduino Nano-MMA8452Q 3-osni 12-bitni/8-bitni digitalni merilnik pospeška: 4 koraki

Arduino Nano-MMA8452Q 3-osni 12-bitni/8-bitni digitalni merilnik pospeška: MMA8452Q je pameten, triosni, kapacitivni, mikroobdelovalni merilnik pospeška z nizko porabo energije z 12 bitovi ločljivosti. Prilagodljive možnosti, ki jih lahko programira uporabnik, so na voljo s pomočjo vgrajenih funkcij v merilniku pospeška, ki jih je mogoče konfigurirati na dve prekinitvi
Raspberry Pi - ADXL345 3 -osni merilnik pospeška Java: 4 koraki

Raspberry Pi-ADXL345 3-osni merilnik pospeška Java Digitalni izhodni podatki so oblikovani kot 16-bitni dvojčki, ki se dopolnjujejo in so dostopni prek digitalnega vmesnika I2 C. Meri
Raspberry Pi MMA8452Q 3-osni 12-bitni/8-bitni digitalni merilnik pospeška Python Vadnica: 4 koraki

Raspberry Pi MMA8452Q 3-osni 12-bitni/8-bitni digitalni merilnik pospeška Python Vadnica: MMA8452Q je pameten, triosni, kapacitivni, mikroobdelovalni merilnik pospeška z nizko porabo energije z 12 bitovi ločljivosti. Prilagodljive možnosti, ki jih lahko programira uporabnik, so na voljo s pomočjo vgrajenih funkcij v merilniku pospeška, ki jih je mogoče konfigurirati na dve prekinitvi
