Predpisovanje očesnega jabolka na recept: projekt BME60B: 9 korakov

2024 Avtor: John Day | [email protected]. Nazadnje spremenjeno: 2024-01-30 12:02

Avtor: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Povečava je ena ključnih lastnosti bralnih očal, ki jih razvrščamo po dioptriji. Po podatkih tehnološke univerze v Michiganu je dioptrija goriščna razdalja leče, običajno merjena v mm, v enoti metrov (Michigan Technology University). Ker imajo bralna očala izbočene leče, bi bila goriščna razdalja pozitivna, zaradi česar bi bile pozitivne tudi dioptrije (HyperPhysics). Goriščna razdalja se povečuje, ko se razdalja med objektom oddaljuje od dejanske leče, kar vodi do zmanjšanja dioptrije, ker so obratno sorazmerne. Zato bi bralna očala z dodatno dioptrijo pomagala objektivu povečati pogled, tako da se lahko zdi, da je goriščna razdalja manjša s povečanjem vrednosti dioptrije.

Predstavljena koda bo uporabljena za napovedovanje dioptrije leče z neznanim receptom. Za izračun recepta se uporabljata dva vhoda: fotografija nadzorovanega ozadja brez uporabe leč in druga fotografija istega ozadja, vendar skozi lečo po izbiri. Program bo izmeril popačenje med tema dvema fotografijama. Od tam bomo lahko ocenili dioptrijo leče in ustvarili rezultat, ki si ga bo uporabnik ogledal.

Za to navodilo boste potrebovali:

• Črno-beli vzorec šahovnice, natisnjen na listu papirja velikosti 11x8,5
• Kamera z možnostjo zaklepanja ostrenja
• Stativ ali kaj podobnega za zaščito fotoaparata
• Različni recepti za očala za branje
• MATLAB

1. korak: Fotografirajte

Če želite izračunati povečavo leče, jo morate znati primerjati z dejansko velikostjo predmeta. Za ta projekt bomo povečano sliko primerjali s kontrolno sliko.

Tako je prvi korak, da naredite dve fotografiji iste slike - prvo samo s kamero, drugo pa skozi leče očal za branje, ki jih želite preizkusiti.

Fotografirali boste 8,5 x 11 -palčno črno -belo šahovnico z 1 -palčno mrežo. Kamero nastavite 11 cm stran od šahovnice. Preden posnamete fotografije, se osredotočite na šahovnico.

Fotografirajte šahovnico brez očal za branje. Nato brez premikanja postavite očala za branje pred kamero in naredite drugo fotografijo.

Poskrbite, da se položaj vaše kamere ne premakne med posnetki. Edina stvar, ki bi se morala med fotografijama spremeniti, je prisotnost očal pred kamero.

Ko končate s fotografijami, jih naložite v računalnik.

2. korak: Slike naložite v MATLAB

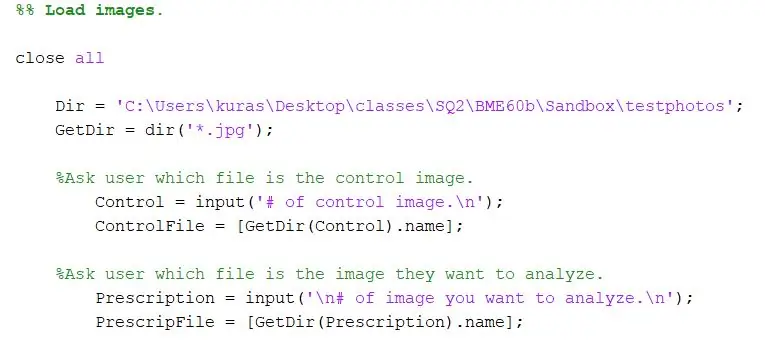
Odprite nov skript.

Najprej določite imenik, v katerem so shranjene fotografije. Nato s funkcijo dir izvlecite slike-j.webp

Dir = 'C: / Users / kuras / Desktop / classes / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');

Za naš projekt smo želeli uporabnika programa pozvati, katere datoteke želi primerjati. Prvi odsek od uporabnika zahteva, da poda kontrolno sliko, drugi pa od uporabnika, naj določi preskusno sliko.

• %Vprašajte uporabnika, katera datoteka je kontrolna slika.
• Control = input ('# kontrolne slike. / N');
• ControlFile = [GetDir (Control).name]
• %Vprašajte uporabnika, katera datoteka je slika, ki jo želi analizirati.
• ChooseFile = input ('\ n# slike, ki jo želite analizirati. / N');
• PrescripFile = [GetDir (ChooseFile).name];

3. korak: Analiza slike

Barvna slika v MATLAB -u je velikosti MxNx3, slika v sivinah pa MxN. To pomeni, da je hitreje izboljšati/urediti sliko v sivinah, ker je manj podatkov za spremljanje. Uporabite rgb2gray za pretvorbo slike v sivine. (Funkcija imrotate je bila uporabljena, ker so bile naše fotografije vodoravne - ta vrstica kode je morda potrebna v vaši različici ali pa tudi ne.)

• %pretvori v sivine in zavrtite
• I = imread (ControlFile);
• I = rgb2gray (I);
• I = imrotiraj (I, 90);

Nato prikažite sliko. Funkcija subplot se uporablja tako, da bo preskusna slika lahko v naslednjih korakih poleg kontrole.

• %prikaz
• slika (1);
• podplet (1, 2, 1)
• imshow (I);
• naslov (ControlFile);

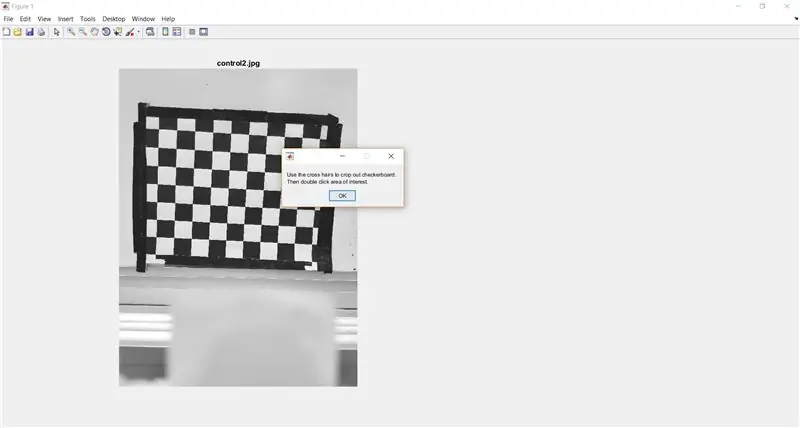
Uporabite imcrop, da uporabnika pozovete, da izreže šahovnico iz celotne slike. Naslednja koda prikazuje tudi polje s sporočilom, ki uporabniku poda navodila.

• %izrežite šahovnico za analizo
• waitfor (msgbox ({'Z navzkrižnimi lasmi izrežite šahovnico.', 'Nato dvokliknite območje, ki vas zanima.'}));
• I_crop = imcrop (I);

Za binarniziranje slike uporabite imbinarize.

I_binary = imbinarize (I_crop);

4. korak: Izračunajte širino belih kvadratov na šahovnici

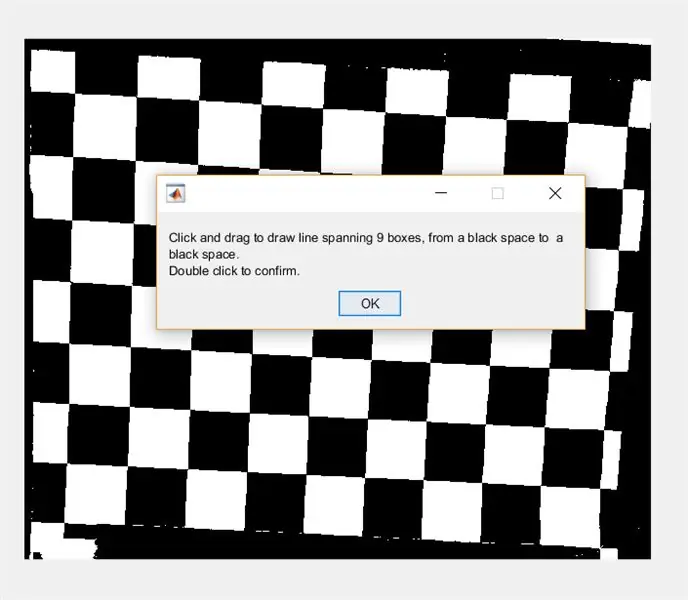
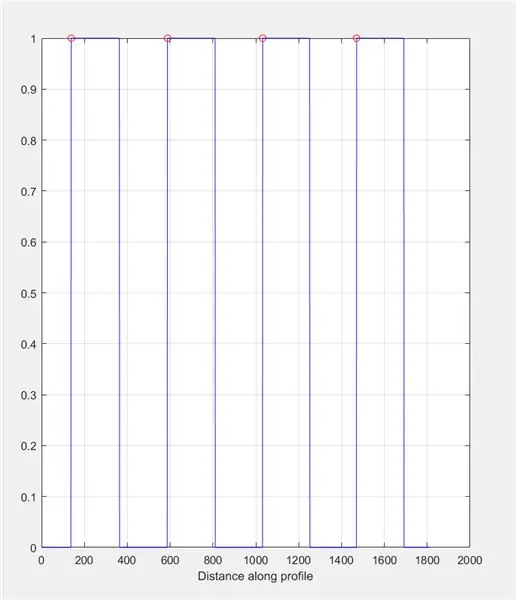
Nato uporabnika pozovite, naj nariše črto čez sliko s pomočjo imline. Ta črta naj poteka vodoravno čez šahovnico. Začeti in končati se mora na črnem kvadratu (ni važno kje)- to je zato, ker bomo merili širino belih kvadratov, ne črnih.

• %črta
• slika (1)
• podplet (1, 2, 1)
• imshow (I_binary);
• waitfor (msgbox ({'Kliknite in povlecite, da narišete črto, ki obsega 9 polj, od črnega do črnega presledka.', 'Dvokliknite za potrditev.'}));
• linija = imline;
• položaj = čakanje (vrstica);
• končne točke = line.getPosition;

Izvlecite koordinate X in Y za končne točke narisane črte.

• X = končne točke (:, 1)
• Y = končne točke (:, 2);

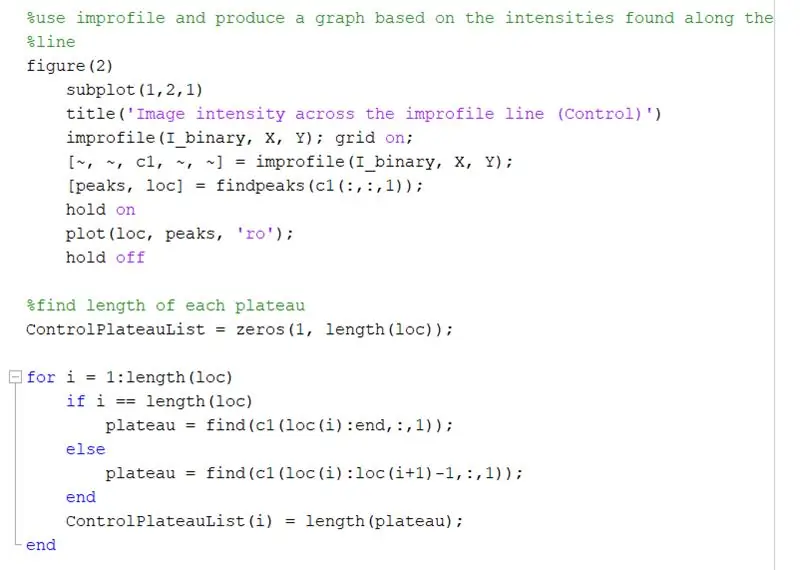
Uporabite improfile za izdelavo grafa na podlagi intenzivnosti, ki jo najdete vzdolž narisane črte. To bi moralo spominjati na kvadratni val v razponu od 0 (črna) do 1 (bela). Izračunajte tudi vrhove in njihovo lokacijo.

• slika (2)
• podplet (1, 2, 1)
• title ('Intenzivnost slike v vrstici improfile (Control)'))
• improfile (I_binary, X, Y); mreža vklopljena;
• [~, ~, c1, ~, ~] = improfile (I_binary, X, Y);
• [vrhovi, loc] = findpeaks (c1 (:,:, 1));
• počakaj
• ploskev (loc, vrhovi, 'ro');
• počakaj

Poiščite dolžino vsakega platoja na grafu improfile z uporabo zanke for. Zaženite zanko for za enako količino vrhov, kot je v grafu improfiliranja. Za izračun dolžine vsakega platoja uporabite funkcijo 'find', da poiščete vse lokacije, kjer je vrednost '1' namesto vrednosti '0'. Nato izračunajte dolžino tega niza, da dobite skupno dolžino platoja, ki bi morala biti enaka širini belega kvadrata v pikslih.

za i = 1: dolžina (loc)

če je i == dolžina (loc)

plato = najdi (c1 (loc (i): konec,:, 1));

drugače

plato = najdi (c1 (loc (i): loc (i+1) -1,:, 1));

konec

ControlPlateauList (i) = dolžina (plato);

konec

5. korak: Ponovite 3. in 4. korak za preskusno sliko

*Opomba: pri risanju improfizirane črte na preskusni sliki jo potegnite čez kvadrate, ki ustrezajo liniji, ki ste jo narisali na kontrolni sliki.

6. korak: Izračunajte povečavo leče

Povečane meritve se izračunajo tako, da se povprečje dolžine planote, ki je bila izračunana v 5. koraku, deli s povprečjem dolžine kontrolnega platoja, ki je bila izračunana v 4. koraku. To se izračuna kot 1.0884.

povečanje = povprečje (platoList)/povprečje (ControlPlateauList);

7. korak: Poiščite R-kvadrat in uporabniški recept prek interpolacije

Z uporabo kode:

• md1 = fitlm (glede na recept, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Najdemo lahko vrednost R-kvadrata grafa GivenPresciption (naše leče podane vrednosti) v primerjavi z MagArray (niz razmerij meritev povečave, ki smo jih izračunali prej). Z dovolj visoko vrednostjo R-kvadrata je mogoče sklepati, da obstaja dovolj močna korelacija, ki upravičuje uporabo te metode. V tem konkretnem primeru je bila vrednost R-kvadrat 0,9912, kar kaže na močno korelacijo in je zato pri uporabi te metode upravičeno.

Uporaba funkcije:

Recept = interp1 (MagArray, GivenPrecription, povečava, 'linearno');

Lahko interpoliramo ustrezno vrednost recepta (na osi x) našega razmerja povečave (vrednost na osi y) in ugotovimo, kakšen je recept uporabnika.

Interpoliranje podatkov je pomembno za delovanje te metode, saj nam omogoča, da na podlagi informacij, ki jih imamo, sklepamo o informacijah, ki jih nimamo. Čeprav bi bila najboljša linija tehnično močnejši kandidat za to predpostavko, ustvarjanje meja za zmanjšanje števila izidov ima enak učinek, kot so očala na recept vseeno v postopnih enotnih vrednostih. To je razloženo v kasnejših korakih.

8. korak: Prikaz uporabnikovega recepta na grafu

Z uporabo naslednje kode:

• slika;
• zaplet (DatePrescription, MagArray, '-g')
• počakaj
• zaplet (recept, povečava, 'bp')
• počakaj
• mreža
• legend ('Podatki', 'Interpolirane točke', 'Lokacija', 'SZ')

Lahko narišemo graf, ki prikazuje razmerja povečave proti danemu receptu z zeleno črto in najdene podatke o naši izračunani povečavi v primerjavi z našim interpoliranim receptom z modro zvezdo. Nato legenda označi naslov, os x in os y ter legendo postavi v zgornji levi kot.

9. korak: Zmanjšajte svoj recept

Za zaokroževanje recepta se uporablja naslednja koda:

• če je recept <= 1.125

  CalculatedPrescription = '1.0';

• elseif recept <= 1.375

  CalculatedPrescription = '1,25';

• sicer če je recept <= 1.625

  CalculatedPrescription = '1.5';

• sicer če je recept <= 1,875

  CalculatedPrescription = '1,75';

• sicer če je recept <= 2,25

  CalculatedPrescription = '2.0';

• elseif recept <= 2.625

  CalculatedPrescription = '2.5';

• sicer če je recept <= 3

  CalculatedPrescription = '2,75';

• elseif recept <= 3.375

  CalculatedPrescription = '3.25';

• drugače

  CalculatedPrescription = 'neznano';

• konec

Recept, ki ga najdemo z interpolacijo, ne odraža nujno dejanskega recepta - to je zato, ker bodo pri analizi fotografije zaradi človeške napake vedno prihajale do majhnih odstopanj. Zato potrebujemo ta korak za razvrstitev dejanskega recepta.

Predpisani recepti se običajno začnejo od 1,0 dioptrije in se v receptih povečajo za 0,25, zato želimo po izračunu recepta določiti recept, ki najbolj ustreza tistemu, kar bi uporabnik morda potreboval. Po izračunu recepta ga poženemo skozi podane stavke If, da preverimo njegovo vrednost in ugotovimo, kateri recept je potreben. Če je manj ali enako 1,125, potem je recept 1,0. Če je manj ali enako 1,375, je recept 1,25. Če je manj ali enako 1,625, je recept 1,5. Če je manj ali enako 1,845, je recept 1,75. In tako naprej.

Vrednosti se nam povečujejo, saj preverjamo, ali so vrednosti manjše od. Če bi zmanjšali vrednosti, bi prvi stavek if ves čas bral prvi stavek if. Če je recept najmanjši, ga želimo takoj prepoznati kot najmanjšega, zato smo najmanjšo vrednost začeli. Vse, kar je višje od najvišje vrednosti, pomeni, da recept ni v dosegu z našimi podatki, zato bo odčitalo niz »Neznano«.